Az 1997-98.
tanév versenyfeladatai
1. FELADAT: PÁROS ÉS NYER!
A következõ feladat megoldását legalább
30 szóban angolul, franciául, németül, olaszul
vagy spanyolul adjátok meg!
( 10 pont )
Margot hä lt in einer Hand
eine gerade Anzahl und in der anderen Hand eine ungerade Anzahl von Münzen.
"Multipliziert die Anzahl der Münzen in Eurer rechten Hand mit
zwei'', sagt Nicolas Chuquet zu Margot.
''Sodann zä hlt Ihr die Anzahl
der Münzen in Eurer linken Hand hinzu und nennt mir die Summe. Ich
werde Euch dann sagen, in welcher Hand sich die gerade Anzahl von Münzen
befindet.''
Erklä re die Methode
von Nicolas Chuquet.
Margot has got an even number of coins in one hand and an odd number
of coins in the other one. In order to find which hand the even number
of coins is in, Nicolas Chuquet says: ''Multiply the number of coins of
the right hand by two, add it to the number of coins of the left hand and
give me the result. ''
Explain Nicolas Chuquet's method
En una mano, Margot tiene un número par de monedas, y en la otra
un número impar de monedas.
Nicolas Chuquet le dice a Margot: ''Multiplique usted or por dos el
número de monedas que tiene en la mano derecha y sume a ello el
número de monedas de la mano izquierda. Dígame cuál
es el total y le diré en qué mano tiene el número
par de monedas.''
Explica el método de Nicolas Chuquet.
Margot ha in una mano un numero pari di monete e nell'altra un numero
dispari. Al fine di trovare in quale mano ci sia il numero pari di monete,
Nicolas Chuquet afferma:''Moltiplicate il numero delle monete della mano
destra per due, aggiungetevi vi il numero delle monete contenute nella
mano sinestra e ditemi il risultato.''
Si spieghi il metodo di Nicolas Chuquet
Margot a dans une main un nombre pair de piece et dans l'autre un nombre
impair de piece. Pour deviner en quelle main est le nombre pair de piece,
Nicolas Chuquet dit á Margot: "Multipliez le nombre de pieces de
la main droite par 2, ajoutez- y le nombre de pieces de la main gauche
et donnez-moi le resultat."'
Expliquer la méthode de Nicolas Chiquet.
2. FELADAT: NÉGYZETRE FEL!
Etienne kivágja az alábbi, A, B, C és D-vel jelzett
puzzle darabokat.
Az A, B és C elemekbõl egy négyzetet rak ki, majd
hirtelen felkiált:
- Hiszen mind a négy elem felhasználásával
is kirakható négyzet!
Rajzoljátok le a válaszlapra mindkét négyzetet,
és jelöljétek meg rajta a puzzle elemeket!
( 5 pont )
3. FELADAT: A KUPA MEGTELT
Lucas születésnapját ünnepli. Azt tervezi,hogy
pezsgõs kupákból egy gúlát épít,
s a legfelsõbe úgy tölt majd pezsgõt, hogy az
kifolyjon, s megtöltse a többi poharat.
A tervezett gúla alapja egyenlõ oldalú háromszög.
Mindegyik kupa az egy emelettel lejjebb lévõ 3, egymást
pároként érintõ kupán áll.
Már majdnem kész a mû, amikor a legutolsó
pohár kicsúszik a kezébõl és eltörik.
Szerencse a szerencsétlenségben, hogy a megmaradt poharakból
azért sikerült Lucas-nak egy négyzet alapú, az
eredetinél egy emelettel kisebb gúlát építeni.
Hány kupája volt eredetileg?
( 10 pont )
4. FELADAT: SZILVESZTER PÁPA ABAKUSZA
Az ábrán látható abakuszt Gerbert d’Aurillac,
a X. században élt matematikus, a késõbbi II.
Szilveszter pápa használta szorzásra.
Egy font (L ) húsz sillinggel
(s) volt egyenértékû, s egy
silling 12 dénárt (d) ért.
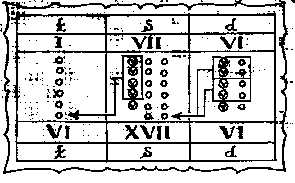
Az ábra azt szemlélteti, hogyan szorozták V-tel
az I font VII silling VI dénárt!
Szemléltessétek ugyanilyenábrán,hogy miként
szorozzuk meg VIII-cal a VII font VII silling VII dénárt!
(5 pont )
5. FELADAT: A REJTETT GÚLA
A gúla térfogata éppen harmada az azonos alapú
és magasságú hasábénak. A gyakorlatban
is szemléltessük az alábbi módon.
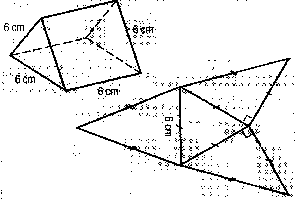
Vegyünk egy szabályos háromszög alapú
egyenes hasábot, amelynek oldallapjai négyzetek. Minden él
6 cm hosszú. E hasáb három, egyenlõ térfogatú
gúlára bontható.
A rajzon látható egy ilyen hasáb képe,
és a három gúlából kettõnek a
hálózata.
A harmadik gúla hálózatát rajzoljátok
le a válasz lapra valódi nagyságban!
( 10 pont )
6. FELADAT: LEHET EGY TÉGLÁVAL
TÖBB?
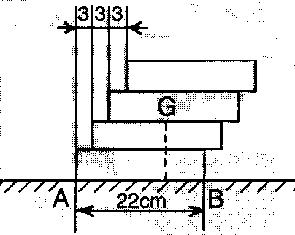A vízszintes talajon Thierry téglákat helyez egymásra
és összeragasztja azokat. A téglák egyformák,
22 cm hosszúak. Úgy helyezi egymásra a téglákat,
hogy azok 3-3 cm-rel eltolódnak hosszanti irányban.
.Legfeljebb hány téglát tud így Thierry
egymásra helyezni, ha az így keletkezett test mindaddig nem
dõl fel, ameddig a szimmetria középpontja az AB szakasz
fölött van?
( 5 pont )
7. FELADAT: HÁNYAT ÜTÖTT
AZ ÓRA?
Marie kirándul. Éppen egyenlõ távolságra
van a két falutól, amikor pontosan egyszerre megszólal
mindkettõben a harang. Mindig annyit üt a harang, ahány
óra van.
Az egyik falu harangja 4 másodpercenként, a másiké
5 másodpercenként kondul egyet.
Marie csak akkor tudja megkülönböztetni a két
harang hangját, ha legalább 1 másodperc különbséggel
kondulnak meg.
Hány óra van, ha Marie 13 harangütést hallott
összesen?
( 10 pont )
8. FELADAT: ADJUNK ÖSSZE !
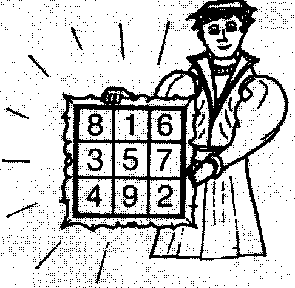Íme egy bûvös négyzet: a sorokban, oszlopokban
és a két átlóban levõ számok
összege mindig ugyanaz.
Helyezzétek el a 9 számjegyet úgy, hogy a nyolc
összeg mind különbözõ legyen!
( 5 pont )
9. FELADAT: NIKOMEDÉSZ CONCHOIDJA
A szögharmadolás problémáját - mai tudásunk
szerint - az ókori görög matematikusok vizsgálták
elõször, s nem találtak olyan eljárást,
mely bármely szög esetén körzõvel és
vonalzóval szerkesztette volna meg az adott szög harmadát.
Nikomedész azonban i.e. 150-ben talált egy olyan geometriai
eljárást, amely során felhasznál egy conchoid
nevû görbét.
A conchoidot az alábbi módon tudjátok megszerkeszteni:
a) Rajzoljátok meg a válasz lap hosszabbik szimmetria
tengelyét! Nevezzük d-nek ezt az egyenest.
b) A rövidebb szimmetria tengelyen vegyetek fel egy A pontot 2
cm-re a d bal oldalán!
c) Válasszatok egy P pontot a d egyenesen, és jelöljetek
ki egy M és egy M' pontot az AP egyenesen 6-6 cm-re P-tõl,
ha ez lehetséges!
Az így kapott M és M' a conchoid egy-egy pontja.
d) Ismételjétek meg a c)-ben leírtakat változtatva
P helyzetét!
Szerkesszétek meg a conchoid mindkét ágát
pontonként amilyen hosszan csak lehetséges!
( 10 pont )
10. FELADAT: ÉS MOST HARMADOLJUNK!
Nikomedész felfedezett egy eljárást, amely segítségével
szöget tudunk harmadolni.
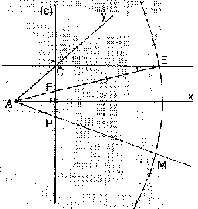
Íme az eljárás: az ábrán látható
xAy szöget szeretnénk harmadolni.
Vegyünk fel egy C pontot az Ay szögszáron,
majd állítsunk C-n keresztül merõlegest az Ax
szögszárra. Legyen ez d.
A d tetszõleges P pontját kijelöljük, s az
AP félegyenes azon pontja lesz a conchoid M pontja, amelyre PM=
2AC.
A C-n átmenõ, d-re merõleges egyenes E-ben metszi
a conchoidot.
Bizonyítsátok be, hogy az xAE szög az xAy szög
harmada! A conchoid definícióját a 9. feladatban megtaláljátok.
( 15 pont )
11. FELADAT: MASZKOT FEL!
Michel, Paul és Jean készülõdnek
a farsangra. Három jelmez áll rendelkezésükre:
bohóc, kalóz és szellem maszk.
Paul mondja:
- Ha Jean bohócnak öltözik, én kalóz
leszek! De ha Jean lesz a kalóz, akkor én inkább szellem
leszek.
Mire Michel is megszólal:
- Ha Paul nem bohócnak öltözik be, akkor én
leszek a kalóz!
Melyik fiú milyen jelmezbe öltözött?
12. FELADAT: SZÜRET!
Germain gazdának két parcelláján indul a szüret.
Az egyiknek a területe kétszerese a másikénak.
Az elsõ napon a teljes szüretelõ brigád a
nagyobbik parcellán dolgozik. A második napra két
egyenlõ létszámú munkacsoportra bomlanak, s
az egyik csapat marad a nagy, míg a másik átmegy dolgozni
a kisebb parcellára.
A második nap végére a nagy parcellát teljesen
leszüretelik, nem így a kis parcellát, amelynek teljes
leszüreteléséhez két embernek egy teljes napi
munkájára volt még szükség.
Feltételezzük, hogy a szüretelõk azonos tempóban
dolgoznak, s a munkanapjuk hossza is azonos.
Hány tagja volt a szüretelõ brigádnak ?
( 10 pont )
13. FELADAT: FILTERES KÁVÉ
Pierre kávéfõzõjébõl kifogyott
a szûrõpapír. Egy olyan négyzet alakú
szalvétából hajtogat egyet, amelynek oldala 21 cm.
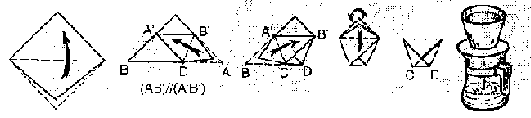
A hajtogatást az ábra szerint végzi.
Készítsétek el a hajtogatást, majd ragasszátok
fel a válasz lapra! Igazoljátok, hogy az A'B'AD és
A'B'CB rombusz, majd számítsátok ki a CD hosszát!
( 15 pont )
